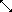
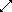
How many unique ways are there to unfold a cube? By unique, we mean that each pattern unfolded cannot be rotated or reflected to get another pattern.
If you look at the corner of a cube, you can unfold it in (at least) three different ways to get the following pattern:
Thus, to go from one pattern configuration to another, all one has to do is to slide a side from one position to another, while keeping at least one side connected.
Note: In actuality, for the proper sides to match correctly, we wouldn't really be sliding the square, but pivoting it at a right-angle around a corner.
Start with the simplest pattern of all, by unfolding two opposite sides of a cube and unrolling the rest to get a T-shaped pattern. From there on, we slide any side across another to get almost all other patterns for a total of 10.
However, the last pattern (grey) is unobtainable through this approach for a total of 11. Thanks to Dirk Bell for pointing that out.
Note: For the 10 patterns obtained by sliding, the width is equal to 3 squares and the height is equal to 4. For the grey pattern, the width is equal to 2 squares and the height is equal to 5. The six squares are left (L), right (R), front (F), back (B), and top (T). The bottom square is left blank.
| L | B | R | L | B | L | B | L | B | ||||||
| ↔ | R | ↔ | ↔ | |||||||||||
| F | F | F | R | F | ||||||||||
| T | T | T | T | R | ||||||||||
| ↕ | ↕ | 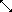 |
||||||||||||
| B | B | L | B | |||||||||||
| L | R | ↔ | L | |||||||||||
| F | F | R | F | R | ||||||||||
| T | T | T | ||||||||||||
| T | ↕ | ↕ | 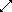 |
|||||||||||
| B | B | B | B | |||||||||||
| L | L | R | ↔ | L | ↔ | L | ||||||||
| F | F | F | R | F | R | |||||||||
| R | T | T | T | |||||||||||